Project Overview: This post explores the implementation of Alternating Direction Method of Multipliers (ADMM) for pruning lightweight Deep Neural Networks (DNNs). We compare this optimization-based approach against traditional magnitude-based pruning on the CIFAR10 dataset.
Introduction
Deep neural networks (DNNs) have achieved remarkable performance across various domains, but their high computational and memory costs often hinder deployment on resource-constrained devices. Weight pruning has emerged as an effective strategy to reduce model complexity while preserving performance.
This project implements ADMM-based pruning on lightweight architectures (MobileNetV2, MobileNetV3) and compares it against a magnitude-based baseline. While heuristic methods are simple and effective, ADMM offers a principled mathematical framework for enforcing sparsity.
Methodology
1. The Heuristic: Magnitude-Based Pruning
Magnitude-based pruning operates on the assumption that weights with the smallest absolute values contribute the least to the network’s predictive capability. The objective is to minimize the loss function \(f(W)\) (typically cross-entropy) subject to a cardinality constraint:
\[\min f(W) \quad \text{s.t.} \quad \text{card}(W) \le l\]Where \(l\) is the target number of non-zero weights. This method enforces hard constraints by simply pruning weights after every step.
2. The Optimization: ADMM-Based Pruning
ADMM formulates pruning as a constrained optimization problem. We reformulate the objective by introducing an auxiliary variable \(Z\) and an indicator function \(g(Z)\)that enforces the sparsity set \(S\):
\[\min_{W} f(W) + g(Z) \quad \text{s.t.} \quad W = Z\]The problem is solved using the Augmented Lagrangian:
\[L_{p}(W,Z,U) = f(W) + g(Z) + \frac{\rho}{2} \|W - Z + U\|_F^2\]Where \(U\) represents the dual variables and \(\|\cdot\|_{F}\) is the Frobenius norm. The algorithm proceeds by iteratively updating \(W\), \(Z\), and \(U\), where \(Z\) is projected onto the sparsity set \(S\) via Euclidean projection.
Experimental Setup
We validated our experiments using the CIFAR10 dataset. We applied the methods to three modern lightweight architectures:
- MobileNetV2
- MobileNetV3-Small
- MobileNetV3-Large
Settings:
- Pruning Ratio: Uniform \(s=0.5\) across all layers.
- Optimization: \(\rho=0.01\), using Adam optimizer with a learning rate of 0.001.
Results
Training Convergence
ADMM exhibited higher training loss and slower convergence compared to the baseline, indicating the difficulty of optimization under strict sparsity constraints.
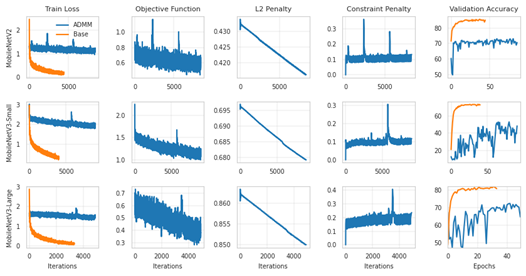 Figure 1: Comparison of Training Objective and Validation Accuracy.
Figure 1: Comparison of Training Objective and Validation Accuracy.
Accuracy Comparison
The table below summarizes the performance before and after pruning. While the baseline consistently had higher pre-pruning accuracy, ADMM achieved competitive or higher accuracy after pruning for certain models.
| Model | Method | Pre-Pruning Acc (%) | Post-Pruning Acc (%) |
|---|---|---|---|
| MobileNetV2 | Base | 10.00 | 70.60 |
| ADMM | 80.66 | 67.10 | |
| MobileNetV3-Small | Base | 48.33 | 64.57 |
| ADMM | 72.47 | 68.48 | |
| MobileNetV3-Large | Base | 35.97 | 35.97 |
| ADMM | 85.06 | 60.13 |
Notably, for MobileNetV2, the baseline substantially outperformed ADMM. This suggests that the larger model size amplified the optimization challenge, causing ADMM to struggle with the increased architectural complexity.
Weight Distributions
We analyzed the weight distributions to understand the pruning behavior.
- Baseline: Exhibits an approximately normal distribution; pruning removes weights near zero.
- ADMM: Many weights are driven exactly to zero during optimization. After pruning, the distribution becomes multimodal, suggesting a sharper separation between important and unimportant weights.
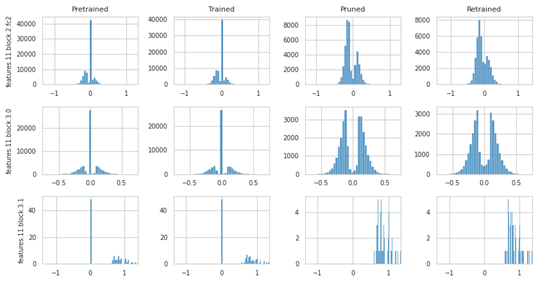 Figure 2: Weight distribution of ADMM method showing multimodal separation.
Figure 2: Weight distribution of ADMM method showing multimodal separation.
Conclusion
This project highlights the trade-offs between heuristic and optimization-driven pruning:
Key Findings:
1. Structured Sparsity: ADMM can induce sharper sparsity patterns and potentially better accuracy on specific architectures.
2. Optimization Difficulty: ADMM introduces significant stability challenges, characterized by slower convergence and lower pre-pruning accuracy.
3. Complexity Sensitivity: The method struggled with the larger MobileNetV2 model, indicating it may require improved optimization strategies for more complex architectures.
Overall, while ADMM is a principled framework, it is not yet reliably effective for all lightweight architectures compared to the simple magnitude-based baseline.
For the full code and implementation details, check out the GitHub Repository.