Project Overview: This post explores the experimental application of 1-Lipschitz layers—typically used to certify robustness in classification tasks—to the more complex domain of object detection. We analyze the trade-offs between robustness, expressiveness, and accuracy using the SVHN dataset on a custom Tinier SSD architecture.
Introduction
Deep learning models are notoriously vulnerable to adversarial attacks, where imperceptible perturbations in input data can cause drastic failures in prediction. While research has successfully leveraged Lipschitz continuous functions to bound model behavior and guarantee robustness in classification tasks, this approach remains largely unexplored for object detection.
Object detection presents a unique challenge: unlike classification, which assigns a single label to an image, detection involves both regression (bounding boxes) and classification (labels) simultaneously.
This project implements SDP-Based 1-Lipschitz Layers within a Tinier SSD Macro Architecture to test if we can bound the model’s global Lipschitz constant and certify robustness against L2-based Projected Gradient Descent (PGD) attacks.
Methodology
1. The Theory: Lipschitz Continuity
A function \(f: \mathbb{R}^n \to \mathbb{R}^m\) is Lipschitz continuous if it satisfies:
\[\|f(x) - f(y)\| \le L \|x - y\| \quad \forall x, y \in \mathbb{R}^n\]Here, \(L\)is the Lipschitz constant, representing the upper bound of the output change relative to the input change. By constraining\(L=1\) (1-Lipschitz), we can theoretically guarantee that small input perturbations result in bounded output changes, ensuring stability.
2. The Architecture: Tinier SSD
We adopted the Tinier SSD architecture, a lightweight version of the Single Shot Detector. To integrate robustness, we replaced standard convolutional layers with SDP-Based Lipschitz Layers.
However, a core challenge arose: 1-Lipschitz layers often require input and output channels to match, which conflicts with the expanding and contracting feature maps of a detection backbone. To remedy this, we utilized Normalized Convolutional Layers at the very start (to expand channels) and very end (to match prior boxes) of the network.
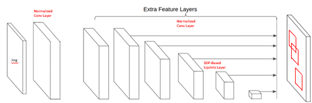Figure 1: Tinier SSD Architecture integrating Lipschitz layers with normalized entry/exit layers.
3. Layer Configurations
We compared three specific layer configurations to analyze the trade-off between strict mathematical robustness and practical performance:
- Spectral-Norm-Based Layers: Fully 1-Lipschitz (most restrictive).
- Standard Convolutional Layers: Unbounded (control/high expressiveness).
- L2-Normalized Layers: Weights normalized by L2 norm (experimental balance).
Experimental Setup
- Dataset: Street View House Numbers (SVHN), chosen for its simplicity relative to COCO/PascalVOC given the high training cost of Lipschitz models.
- Attack: Custom L2-based PGD Attack (Projected Gradient Descent) with \(\epsilon=0.5\).
- Hardware: Trained on RTX 4090.
Results
Accuracy & Robustness Trade-off
We evaluated the models on clean data vs. adversarial data. The results highlight the difficulty of applying strict constraints to complex tasks.
| Configuration | Clean mAP (%) | Adversarial mAP (%) | Observations |
|---|---|---|---|
| Naïve (Baseline) | 78.79 | 42.07 | High accuracy, but severe drop under attack. Inconsistent predictions. |
| Spectral-Norm | 0.00 | 0.00 | Infeasible. The constraints were too restrictive for the model to learn detection features. |
| Standard Conv | 78.67 | 58.60 | High expressiveness, generated many false positives. |
| L2-Normalized | 61.75 | 52.63 | Lowest drop in accuracy. Most consistent predictions with minimal false positives. |
Visual Analysis
The visual results clarify the numerical metrics. The Naïve model (Figure 2) shows high variance and erratic bounding boxes under attack.
Figure 2: Naïve Model - Clean (Left) vs Adversarial (Right).
In contrast, the L2-Normalized model (Figure 3) maintained the highest consistency. While its raw mAP was lower, it resisted the generation of hallucinations (false positives) better than the Standard Conv configuration.
Figure 3: L2-Normalized Model - Clean (Left) vs Adversarial (Right).
Lipschitz Constant Analysis
We analyzed the Lipschitz constant across layers for the “Standard Conv” configuration. The global Lipschitz constant reached ~95, driven largely by the unbounded first and last layers. Interestingly, the constant increases as the network gets deeper, particularly in the classification heads.
Figure 4: Analysis of Lipschitz constants across network layers.
Novel Insights
Key Findings:
-
The “Fully 1-Lipschitz” Barrier: Implementing a fully 1-Lipschitz network (via spectral norm) for object detection is currently impractical. The constraints destroy the expressiveness required for regression and classification simultaneously.
-
Consistency vs. Accuracy: While the L2-Normalized layers did not achieve the highest mAP, they offered the best stability. The drop in accuracy between clean and attacked data was minimal compared to other models.
-
Parameter Efficiency: A massive 7M parameter partially-bounded Lipschitz model was outperformed by a tiny 338k parameter Naïve model on clean data. This suggests that simply scaling up model size cannot compensate for the restrictiveness of Lipschitz bounds without new architectural innovations.
Conclusion
This work establishes a baseline for applying Lipschitz continuity to object detection. While fully certifying robustness remains a challenge due to expressiveness constraints, L2-normalization offers a promising path for reducing false positives and stabilizing predictions against adversarial attacks.
Future work should explore layers that are “mostly” 1-Lipschitz to balance expressiveness or investigate these constraints on segmentation tasks, where pixel-based attacks are most prevalent.
For the full implementation and code, check out the GitHub Repository.